Competing Theories of Spherical Trigonometry

At around the same time that the first reliable translation of Menelaus’ Spherics was being made by Isḥāq ibn Ḥunayn (c. 830–c. 910) and Thābit ibn Qurra (c. 830– 901), Thābit himself wrote a separate treatise on the fundamental theorem of Greek spherical trigonometry, Treatise of the Sector Figure (Kitāb al-shakl al-qaṭṭāʿ), which was based on a convex quadrilateral made of arcs of great circles. Shortly after this, Abū al-Wafāʾ al-Būzjānī (940–998) and Abū Naṣr Manṣūr ibn ʿIrāq (c. 950–c. 1036) produced new theorems based on the trigonometric functions: sine, cosine and tangent, which had been adopted from Indian sources. Finally, in the tenth and thirteenth centuries, the two great polymaths Abū Rayhān al- Bīrūnī (973–1048) and Nasīr al-Dīn al-Ṭūsī (1201–1274) wrote two treatises that would set spherical trigonometry on a solid foundation as an independent branch of mathematics. These were Treatise on the Keys to the Science of Cosmography (Kitāb maqālīd ʿilm al-hayʾa), and Treatise of the Sector Figure (Kitāb al-shakl al-qaṭṭāʿ), also known as the Epistle of the Sector in the Science of Geometry (Risālat al-qaṭṭāʿ fī ʿilm al-handasa).

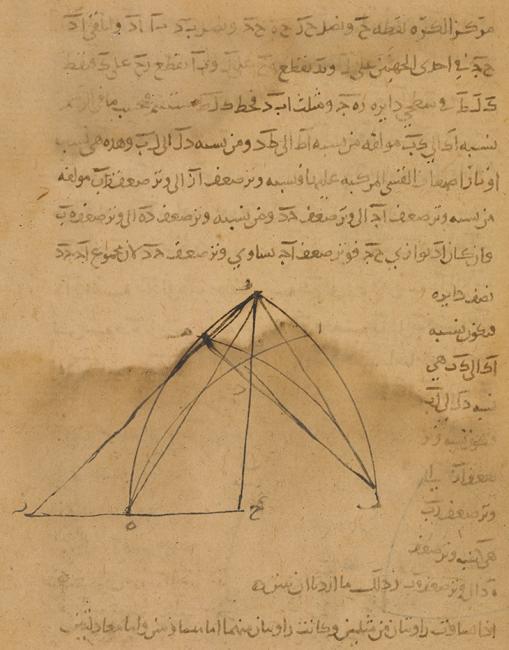
However, not all proficient mathematicians were convinced of the superiority of the new methods. In the tenth century Abū Sahl al- Kūhī criticised his contemporaries for thinking that certain spherical problems were more easily solved using the theorems that would replace the Sector Theorem (al- shakl al-qaṭṭāʿ) – namely the theorem that dispenses [with the Sector Theorem] (al-shakl al-mughnī) and the shadow theorem (al-shakl al-ẓillī), which are mathematically the same as our spherical sine law along with its tangent configuration. Indeed, al-Kūhī quite adeptly showed that the problems in question could be efficiently handled by successive applications of the Sector Theorem. Here, we see the interplay of different styles of mathematics – classical methods along with medieval innovations.

Re-reading the Ancient Spherics

The scholars who worked on developing the new spherical trigonometry simultaneously studied the ancient Spherics from a critical perspective and produced new editions of this classic work. Abū Naṣr Manṣūr ibn ʿIrāq (c. 950–c. 1036) produced a new edition of one of the Arabic translations of the text, adding some mathematical and astronomical comments and changing one of the basic objects of spherical trigonometry from the classical chord to the more contemporary sine. Nasīr al-Dīn al-Ṭūsī (1201–1274) later made use of a number of different versions of various manuscripts, producing his revision of the canonical work. This was a brilliant piece of critical scholarship, which treated the convoluted history of the text and included detailed mathematical and astronomical commentaries. This was al-Ṭūsī’s way of paying respect to an important predecessor, whose work he had built on and surpassed in his own Treatise of the Sector Figure – a complete mathematical treatment of plane and spherical trigonometry as a branch of pure mathematics, using both the ancient approach of the Sector Theorem and the new, more fruitful, theorems produced by scholars of the Islamic period.

The Spherics in Latin

About a century before al-Ṭūsī wrote his treatise, Gerard of Cremona (c. 1114– 1187), working in Toledo, Spain, had produced a Latin translation of Menelaus’ Spherics from yet another Arabic version, now lost, which was probably a combination of two known translations. Much later, in the early eighteenth century, Edmond Halley (1656–1742), Savilian Professor of Geometry at Oxford and Astronomer Royal, produced a new Latin version, this time from the Hebrew translation of Jaqob ben Māḥir (1236–1304). It was based on the same Arabic source as Gerard’s Latin, was supplemented with occasional reference to a different, older Arabic version, and made use of the mathematically competent Latin version of Francesco Maurolico (1494–1575). Halley, like Maurolico before him, altered the text in various ways to create something that he believed was mathematically close to whatever Menelaus originally wrote.

The fact that the Spherics was often passed down without much understanding, is also made clear by the Latin tradition. In another manuscript in the British Library, Harley MS 13, we find a fragment of Gerard’s translation. However, the treatise includes no diagrams and breaks off after just a few propositions, making it mathematically useless. In this case, the treatise is a sort of ornament – a cultural artefact meant to decorate, but of little real use.

A Foot in Both Worlds

Mathematical scholars of the ancient and medieval periods did not think of their own, innovative work as completely surpassing those of the past masters. As they developed new mathematical theories and methods, they continued to study, edit and articulate the ancient works – not just as historical relics, but also as valuable sources of mathematical ideas, and as inspiration for the development of their own mathematical style.