Menelaus’ Spherics

Menelaus of Alexandria (active around the turn of the second century CE) wrote his Spherics in a time of flourishing intellectual life under Roman imperial rule. It addressed previous work in spherical geometry, but may never have been seriously studied in its entirety in the ancient period and no Greek manuscript of the text is known.

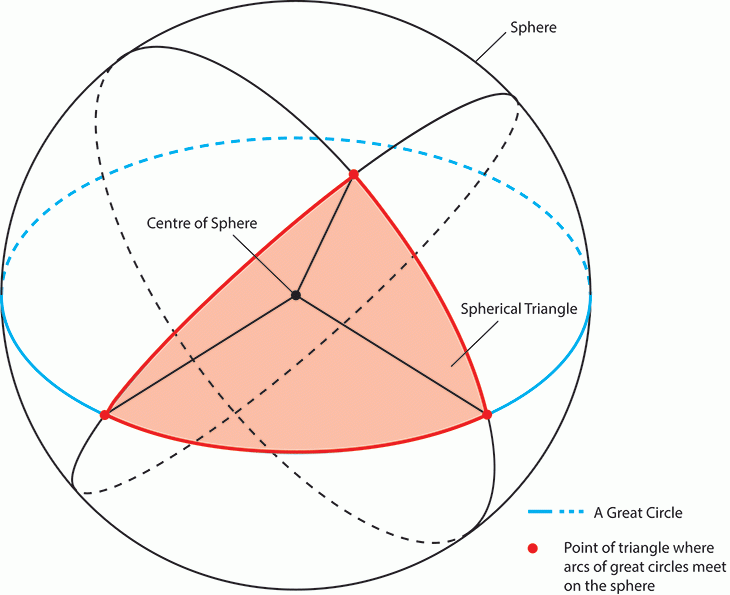
Triangles on a Sphere

The material in the treatise can be divided into three parts. The first part treats the geometrical properties of spherical triangles – triangles whose sides are great circles of the sphere – by developing analogies between these and the properties of plane triangles treated in Euclid’s Elements. The second part shows how arcs (qaws) of spherical triangles can be measured using the lengths of chords dependant on these – mathematically related to the later sine function. This part is based on a theorem often known as the Menelaus Theorem, which during the medieval period was called the Sector Theorem (al-shakl al-qaṭṭāʿ).

The third part shows how the methods of the second part can be applied to solve problems in spherical astronomy – a field that studies issues such as the length of daylight and night-time, or the rising times of stars or arcs of the ecliptic, which can be solved by considering the earth as a very small sphere surrounded by a large, spherical, moving cosmos.

Menelaus’ Spherics was translated into Arabic at least twice during the cultural ferment of the early ʿAbbāsid Caliphate in Baghdad. The original translations of the Spherics have all been lost, but corrections and amalgamations of two of these made by later mathematicians are found in subsequent sources.

A Maze of Medieval Spherics

From the time of its translation, Islamicate scholars worked extensively in the areas of mathematics addressed by the Spherics. Simultaneously, these same scholars studied and re-edited the Spherics itself, making it a canonical text of advanced mathematics education. Abū ʿAbdallāh al-Māhānī (c. 853–c. 866) and Aḥmad ibn Abī Saʿd (or Saʿīd) al-Harawī (c. 956–c. 960) both edited a first, poor translation, which was made through Syriac, or by Syriac speakers. Another, better, translation was made by Isḥāq ibn Ḥunayn (c. 830–c. 910), the son of the great medical translator – himself an important translator of mathematical texts. This version was then edited by Abū Naṣr Manṣūr ibn ʿIrāq (c. 950–c. 1036).

Our understanding of Menelaus’ mathematics is therefore derived from a tangled web of these and further versions of the Spherics, most of which were produced at a time when the text was still a living source of new ideas.

Stories in Manuscripts and Diagrams

British Library manuscript Or. 13127 contains al-Harawī’s recension of the Spherics copied out by someone named Ismaʿīl in Damascus on 4 Rabī’ al-Thānī 548 (29 June 1153). Ismaʿīl tells us that his transcription was made from a copy owned by a relatively well-known mathematical scholar, Ibn al-Sarī ibn al-Ṣalāḥ, who died the year after this manuscript was copied. Since the manuscript contains a number of Ibn al-Ṣalāḥ’s mathematical comments, it is tempting to believe that Ismaʿīl was his student. Nevertheless, an inspection of the diagrams in the manuscript sheds light on the early transmission of the treatise and gives us important clues about how this manuscript was actually used.

Following the Menelaus text there is an almost complete set of separate diagrams that are titled ‘Figures of the Treatise of Spheres by Menelaus, transcribed from a copy that was not corrected, but was translated based on the first composition.’ Interestingly, about a third of the way through the text, these earlier diagrams have been copied into the al-Harawī treatise, in such a way that the diagrams and letters often fail to match the text – making it unlikely that this manuscript was ever seriously studied in its entirety. In this state, the manuscript was used as scrap paper by a certain Fatḥ al-Dīn ibn Muẓaffar al-Ṣiddīqī, at the Mosque of Sultan al-Ghūrī in Cairo in 1509, to write out some passages of rational theology and a table of dry measures of the sort that we find in elementary educational texts in Egypt spanning many centuries and multiple languages.

Although it is clear that throughout its history few people actually studied the various manuscripts of this canonical work, the significance of its approach to spherical geometry meant that serious mathematicians continued to revise and edit the text, and it served as an enduring source of inspiration for their original work in spherical geometry.