Translating a Work of Higher Mathematics

Slicing up a Cone

Apollonius of Perga (late third–early second century BCE) was the intellectual heir to the Hellenistic tradition of Greek geometry, following in the footsteps of Euclid (late fourth–early third century BCE) and Archimedes (third century BCE). We are told that he studied with the students of Euclid in Alexandria, on the Nile Delta, and it was here that he worked out a new, more general approach to conic theory, by cutting arbitrary cones with planes and using the geometry of these so-called conic sections to determine the mathematical properties of the parabola, ellipse, and hyperbola – which curves he also named.

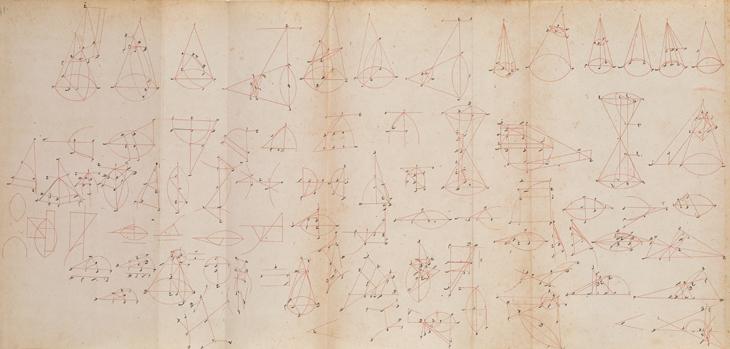
He wrote this work up in a treatise of eight books, known simply as the Conics. It was meant to do for conic theory what Euclid’s Elements had done for the theory of plane geometry. The first four books set out the fundamentals of conic theory, while the next three developed methods for using the properties of these curves to solve geometrical problems that could not be solved by plane methods. Unfortunately, the eighth book, in which Apollonius actually solved various problems, has been lost. In fact, the absence of this book excited the imagination of a number of mathematicians over the centuries – Ibn al-Haytham (965 to c.1040) wrote a Tract on the Completion of the Conics (Maqālah fī tamām kitāb al-mukhrūṭāt) in the middle years of his life, and Edmond Halley (1656–1742) included his own reconstruction of the eighth book along with his 1710 Latin translation of the Greek and Arabic texts.

The difficulty of the Conics, however, meant that it was little studied in Greco-Roman antiquity, and the only Greek version of the text that survives is an edition of the first four books made by Eutocius of Ascalon (late fourth–early fifth century CE). Hence, the Arabic translation was not only vital for Islamicate mathematicians who sought to push conic theory to new applications – such as the solution of third degree equations – it is also essential for our understanding of Apollonius’ original approach.

A Collaborative Translation Project

Apollonius’ Conics was translated over the course of some years or decades by a group of scholars centred around Baghdad. In their introduction to the finished translation, Kitāb fī al-makhrūṭāt, the Bānū Mūsā – Muḥammad, Aḥmad, and al-Ḥasan (ninth century CE) – give us one of the most vivid first-hand accounts that we possess of the working practices of the ʿAbbāsid translators.

They begin by pointing out that even in antiquity the text was little read and less understood so that by the time of Eutocius it had undergone much corruption – which, the Bānū Mūsā tell us, is the fate of all difficult treatises. Eutocius then restored the first four books, using methods that the Bānū Mūsā praise but do not explain. By their own time, however, they assert the science of geometry was again in such a sorry state that hardly anyone understood even the basics of Euclid’s geometry.

Somehow, the Bānū Mūsā got their hands on a single manuscript of the Greek text in a version prior to Eutocius’ corrections. They say that they tried to translate and study the text, but since they were not scholars of Greek, they must have had unnamed collaborators who were. At first, however, they could make no headway due to the excessive textual corruption. In fact, the first major advance came not from the Greek source, but through original mathematical research carried out by al-Ḥasan ibn Mūsā. By studying the intersection of a cylinder with a plane, he was able to show that the section is an ellipse, demonstrate its properties, and prove that the curve is also one of the conic sections. Shortly after writing a treatise on his findings, however, al-Ḥasan died.

More progress came fortuitously when Aḥmad ibn Mūsā was assigned to Syria to oversee the postal service (al-barīd). While in Syria, he discovered a copy of Eutocius’ correction, probably accompanied by the latter’s commentary. Aḥmad studied this source and produced his own commentary, presumably again with the help of Greek speaking collaborators. On this basis, he was able to complete his study of the remaining books, once he had returned to Baghdad. Furthermore, he added internal references to the text to make it more intelligible – something that no one had done before. We are then told that Hilāl ibn Abī Hilāl (ninth century CE) translated the first four books and Thābit ibn Qurra (c.830–901) translated the last three.

A Meeting of Many Minds

The translation of Apollonius’ Conics was undertaken in an exciting place and time, in which various “people of the book” (Jews, Christians, Muslims and Sabians) of various ethnic and linguistic backgrounds made a concerted effort to gather, translate and adapt whatever they could find of the world’s accumulated knowledge, in order to lay the groundwork for extending this body of knowledge.

The rare detailed accounts in our sources indicate that the translation of difficult, technical works could be an involved process, taking place over many years through repeated study of manuscript sources, depending on a number of different individuals who contributed their various technical and linguistic strengths.